

春节是中华民族盛大的阴历新年
这是世界上规模最大的节日

在春节前后
炎黄子孙们不远万里背井离乡
与亲人们团圆
在此期间
中国的铁路上会产生
地球上最大规模的人口迁徙

作为世界上最能吃最能玩的种族
聪慧大胆的中国人创造了特别多的娱乐活动
好比
贴对联、放鞭炮、看春晚、接财神、吃饺子……

和……抢红包……

人们抢微信红包的心态是一件很风趣的事
拼死拼活拿了几分钱还冲动到爆炸!
感到就像是一帮人大老远地非常困难欢聚一堂
然后他们一起在垃圾堆里捡矿泉水瓶
假如你在春节期间,乐意阔别微信红包的引诱,戒除自己的手机控,和很久不见的亲戚们聊聊天,看看久违的春节联欢晚会,你很快就会发现,还是微信抢红包最好玩……
看看近三年来的微信红包数据就晓得抢红包有何等火!
去年光大年节一天全国人民就发出了80.8亿个红包!
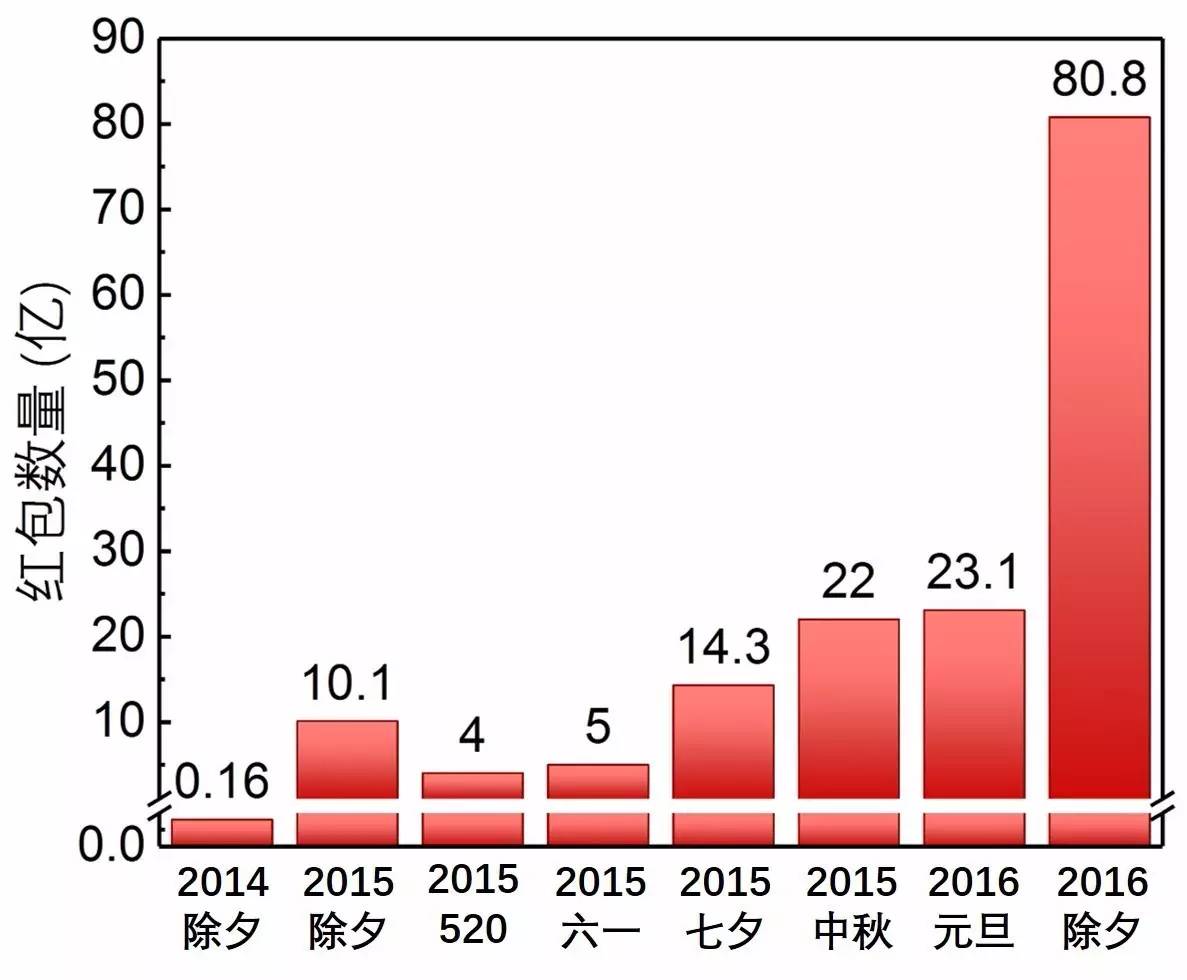
图1. 部分重要节日的全国微信红包数目
抢红包已经超出了红包自己,成了一种独特的社交方法,是中国人在春节前后释放情感、满足心理诉求的重要载体。
抢红包也让很多人深入了解到,自己不只穷、贪心、聒噪、懒散,并且命运也特别蹩脚。
不是吹法螺,我四周没有人敢和我拼抢红包手速。然而作为一个人品差到顶点的人,我常常能在人均几十块的大红包里稳稳地第一个拿下几分钱。
这也许就是稳稳的幸福吧……
信任很多人都和我一样有一些直觉
好比抢红包貌似后抢比先抢能拿到更多的钱?
好比抢红包的金额是和人有关的?
老子要测试也不会给他们测试!
如今国表里关于抢红包的理论研究非常匮乏,虽然很多人都熟悉到了抢红包战略的重要性,但绝大部分人都只逗留在了感性的、经历的层面上!
我想我有必要对抢红包这件大事展开系统的研究,把它提升到理论的高度!并给出抢红包的最优战略!
下头,请大家追随我的思绪,一点点破解抢红包的奥妙。信任等你看彻底文的那一刻,你会成长成一个和我一样优良的红包教父。
一、微信红包,先抢后抢究竟公不公正?
直接先亮出答案
不!公!平!
看到这里很多读者也许会大吃一惊!不公正这还抢个屁啊!那我应当咋办啊!
但微信红包先抢后抢确实是有区其余!
(我们所说的公正,是指随机、平均,先抢后抢没有差别。好比抓阄就是一个典范的公规范则,不顾先抓后抓,每个人抓到的几率和散布都是一样的。)
用一个很简单的抢红包试验便能够证实
好比说有n个人抢一个(n+1)分钱的红包,那结果确定是某一个人抢到2分钱,剩下的人抢到1分钱。
(你说这不空话么……劳资的抽屉原理在小学的时候就已经通关了)
但假如你真的发一个这样的红包你就会发现一个吼神奇的现象!我称之为“末位红包抽屉原理”(Last red bag drawer principle)
末位红包抽屉原理:n个人抢一个(n+1)分钱的红包,必定是前面的人都抢到1分钱,最后一个人抢到那个2分钱!
下头由我和我的4个小号为大家详细展现一下试验结果
(1)2个人抢3分钱,是亚清抢到了2分钱

(2)3个人抢4分钱,最后一个人抢到2分钱

(3)4个人、5个人的情形,结论都是一样的!

过去我们也许天性地认为,微信抢红包不过就是把一个钱随机分成几份,然后随机分给几个抢红包的人。但我的“末位红包抽屉原理”已经充足证清楚微信红包先抢和后抢是有很大区其余!否则就不也许永远只有最后一个人能拿2分钱!
虽然说现实生活中很少会有一个人发几分钱红包而不被打死的情形出现,然而我们的试验已经为摸索微信抢红包的原理迎来了曙光!
二、先抢抢不到大的,后抢才能够抢到大金额?
还是直接先亮出答案
是!这!样!的!
看到这里很多读者也许会大吃两惊!微信怎样会出这么扯的设计!
但假如你细心查查自己抢过的红包就会发现,第一个抢的人永远抢不到很大的数。我称之为“先抢抢不到大红包原理”(First rob rob no big red bag principle)
下头我和我的4个小号为大家带来一组抢红包试验!
【试验内容】我发50块的红包,给5个人抢。红包发了210个,记载每顺序递次1个人抢到的金额。(抢的顺序是通过打乱随机的,以消除人品等搅扰因素。)
结果表示,第一个抢的人抢到的红包金额散布范围是这样的
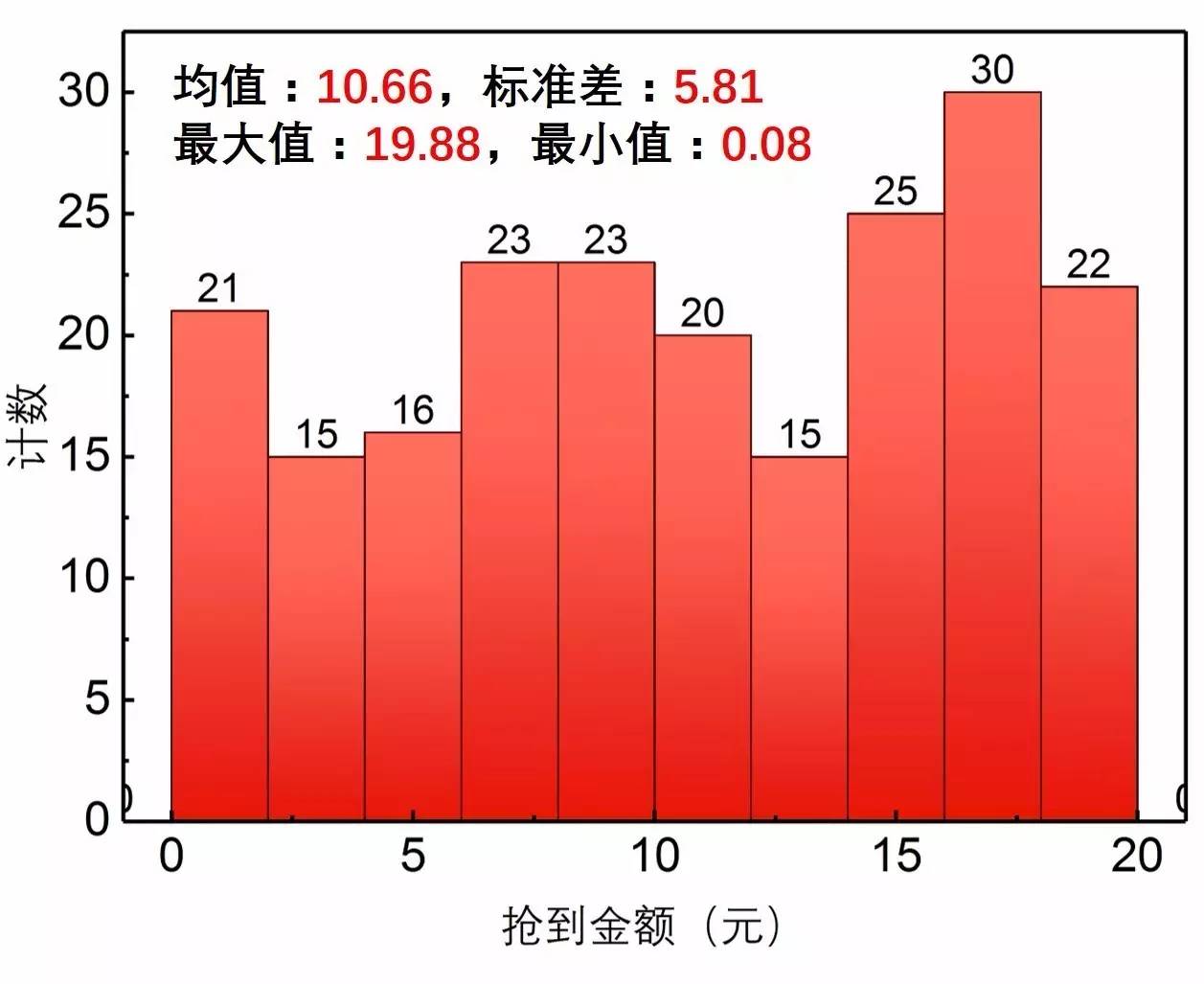
图2. 第一个人抢到的微信红包金额频数散布直方图
发现这其中的诡异的地方了吗?
5个人抢50块红包抢了210次,第一个人居然永远抢不到20块以上的红包!最高只抢到过19.88元!
也就是说,真实的大红包都只会在后面出现,像这样
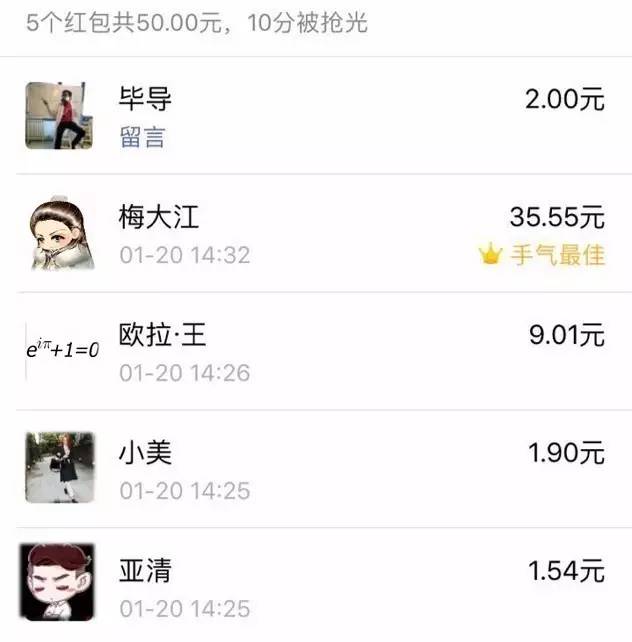
为了进一步研究这其中的规律,我打算了大批资金,发个愉快!
【试验内容】界说5个人的标准顺序:毕导-亚清-小美-欧拉·王-梅大江。轮换他们的顺序,在每种顺序下发50块红包,抢30次,共150次。记载每次5个人抢的红包金额,获得750个原始数据。(以下图所示)

最终获得的五个人抢到红包的金额范围散布是这样的
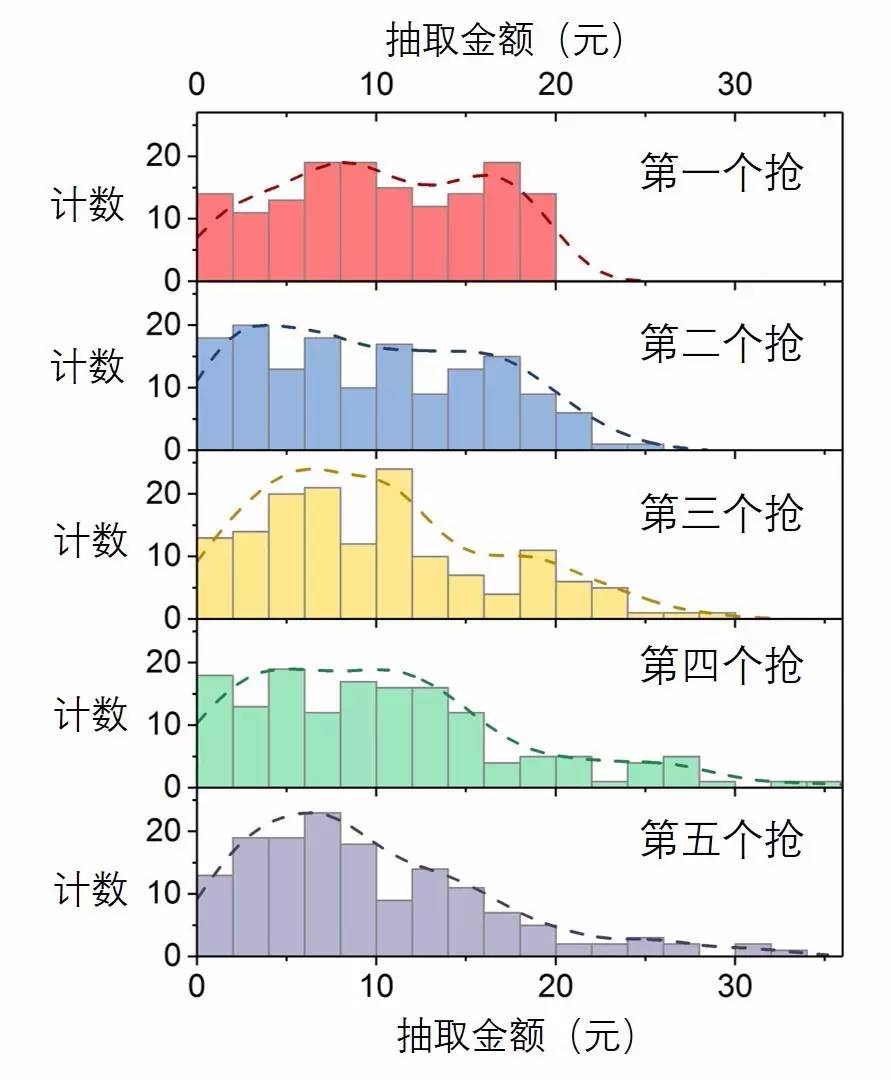
图3. 不一样抢红包顺序抢到的金额频数散布直方图
这张图已经能够告知我们很多规律了
第一个人永远不会超出20元!直接认输吧!
从第三个人开始才委曲能抽到30元以上!
越往后,才越有希望抽到超级大红包!
抽到大红包的几率是很小的(似乎是空话吼)
恐怖!早在2014年我就已经开始暗自用打地鼠游戏练习抢红包,最终习得一身技艺,指如疾风,势如闪电,能够扫平一切群的一切红包,江湖人称“红包轰隆手”!
然而目前看来,“先抢抢不到大红包原理”已经注定了,恰是我超凡的手速让我输在了起跑线上……
我必须要持续探讨出一套最好的抢红包战略!
三、抢红包和人品有关吗?
在进一步试验之前,我认为首先得消除一个因素的搅扰……

世间万物都有它运转的轨则!
理论上讲,你抽SSR和我抽SSR的几率是一样的,你出敬业福的几率和我也是一样的。然而这个世界就是会分出非洲人和欧洲人,就是有人敬业有人不敬业(我已经集齐五福了,我去年也集齐五福了的嘿嘿)
生活中的各种不公正让我们不能够不思考:除过几率以外,还有一种更重要的物品在左右着我们的客观世界——人品!
5个人抢的150个50元红包的结果是这样的

图4. 五个人抢到的金额频数散布直方图
呃……起码五个人都能抽到大红包……脸还不算太黑……那么究竟谁最凶猛呢?请看下头的散点图和表格数据

图5. 五个人抢到的金额
5个人抢50块,平均每人10块钱
从图上能够看出,5个人的平均值都是在10块钱附近,标准差也都在6~7之间。
然而细细看看统计数据还是有显著差别的……
我的平均值只有9块1!小美有10块7!这差距也太尼玛大了吧!
我的手气佳次数也很低!而手气最烂次数排名第一!
综合看来,小美的人品最好,欧拉·王其次然而施展不稳固,下来是梅大江、亚清,人品最差的就是我……也许人品和颜值是成正比的吧……
--“所以微信抢红包这事和人究竟有无关系啊?”
--“人品这类事情,假如能用理论算的话还叫人品吗?”
四、抢红包最优战略是什么!
人品这类虚无漂渺的因素还是撇开不谈了,毕竟大过年的我们也很难在抢红包之前突击扶老奶奶过马路来攒人品(摊手)
抢红包的时候我们唯独能控制的就是先抢还是后抢!另外我记得之前微信群里常常有抢红包的游戏,规则很简单,就是抢到“手气最好”的人要持续发红包
所以接下来我们的研究任务是!
平均抢到的钱是先抢的多还是后抢的多?
抢到钱的动摇是先抢大还是后抢大?
拿到“手气最好”的几率是先抢高还是后抢高?
仍然采用前面的那组试验数据,在五种抢红包顺序下的原始数据是这样的

图6. 五种顺序下抢到的金额
直观上看大家平均都在10块上下动摇
下头我们疏忽人的因素,把五张图的数据汇总到一张图上!

图7. 五种顺序下抢到的金额汇总
规律已经很显著了!
均值:不管先抢后抢,均值都在10左右
标准差:后抢的标准差更大,也许抢到超级大红包,也也许抢到超级小红包
最大最小值:第一个抢的人超可是20,后抢才也许抢到超级大红包
手气:第一个抢的人“手气最好”的几率最高!手气最差的几率最低!
所以抢红包的最优战略以下:
不管先抢还是后抢,抢到的平均金额都是一样的!(你踏马又在说空话吼,不一样还玩个屁啊)
假如你是一个风险躲避者,一个连50块钱都不敢拿来炒股的人,只想要稳稳铛铛地抢,就先抢吧!否则动摇太大,假如你持续抢了好几个1分钱也许就跳楼了。
假如你是一个风险偏好者,只是寻求体验抢到超级大红包的快感,就后抢吧!你也许时不时地爆出一个超级大红包傲视群雄!
假如你想多多抽到"手气最好"证实自己的人品,就先抢!
假如你在玩“手气最好发红包”的游戏,却又只想闷声发大财,就后抢!
看到这里也许有人会质疑,你这不就只做了150个红包试验,样本量太小,得出来的结果也许根本不具有广泛规律啊!
然而横竖大过年的闲得慌,我的探讨固然不会就此停止!
五、微信究竟怎样设计的抢红包?
依照正常的套路,抢红包最简单的方法不就是把红包的总钱数随机分给几个人么……然而微信偏不这么搞,就是必定要让第一个人抽到的钱只能在0.01元到20元之间。
关于5个人抢50块红包而言,20元是个什么数?
在一篇《微信红包的架构设计简介》的文章中提到这也许是“平均值的2倍”(也就是说,每个能抢到的钱最多是如今剩余金额的平均值的2倍)
虽然不领悟微信为何要搞这么复杂的一套规则,然而我们无妨拿数据检验一下这个规则对纰谬!
(以下为理论推导,理科生可快进)
(1)检验第一个人抢到的金额是不是屈服平均散布
简化:抢红包问题自己是(¥0.01,¥0.02,…)的团圆散布,在此为检验平均散布,将其作为持续散布近似处置。
首先对每个人作为首抢时的数据分析,进行Kolmogorov-Smirnov检验,利用积累散布函数检验第一个人抽到的金额是不是屈服平均散布。假定检验均通过,获得相似“毕导第一个抢时,毕导抢到的金额确定是平均散布”的结论。
(2)检验是不是有人品因素的搅扰
看五人分别作为首抢时是不是有个人因素致使抢到金额有散布上的差别,进行Anderson-Darling k-样本检验,发现其实没有。所以抢红包次数足够多的条件下,不存在脸帝光环。
(3)抢到的金额是多少到多少的平均散布?
最小值确定是0了,缘由是实际中已经晓得有人不顾红包金额多大都只能抢到1分钱。
依据统计揣摸的点估量理论中的极大似然估量晓得,参数的极大似然估量是最大值。我们的210组抢红包数据中,第一个人最大就抢到过19.88元。
然而极大似然估量常常低估了,采用贝叶斯估量的方法。先验散布选共轭的帕累托散布,后验均值是mN/(N-1)=210/(210-1)*19.88=19.975。
基本能够在统计学意义上判断,平均散布的右端点是20。
(4)后面抢的人也屈服0.01~剩余均值2倍的平均散布吗?
依据第一个人的平均散布能够递推出第二个人的散布密度函数,进一步用相似方法检验第二个人抢的金额是不是相符这个密度函数。检验相同通过,第二个人的金额屈服0.01~剩余均值2倍的平均散布。固然从算法的简练性上来讲,微信也不太也许给第一个抢和后抢设置不一样的算法规则。所以我们有必定的缘由信任微信红包是按这个规则设计的。
至此基本能够给出微信设计的抢红包规则了:
每个人能抢到的金额屈服0.01到2倍剩余均值之间的平均散布。
我们5个人抢50块:
第一个人最多能抢到2*50/5=20元,好比他抢了5元,此时剩下45元。
第二个人最多能抢到2*45/4=22.5元,好比他抢了12元,此时剩下33元。
第三个人最多能抢到2*33/3=22元,好比他抢了17元,此时剩下16元。
第四个人最多能抢到2*16/2=16元,他和第五个人分这16元。
下头要考虑的问题是:这类规则产生的红包,是不是会致使先抢后抢均值相等,尔后抢的方差更大?
(以下是一大段的理论推导,理科生可快进)
将问题笼统为n个人抢一个S元的红包

证毕,在微信红包的“0.01~2倍剩余均值平均散布”算法下,先抢后抢的均值相同,越往后抢方差越大。最后两个人同散布。
六、闲得蛋疼
目前既然我们已经晓得了微信红包的算法原理……那便能够编程给自己发红包看规律了……
出于礼貌,我用matlab给自己发了五万个红包。五个人抢红包金额散布图是这样的(纵坐标太大隐去了……)

图8. 不一样前后顺序抢到的金额散布图(五万次模仿)
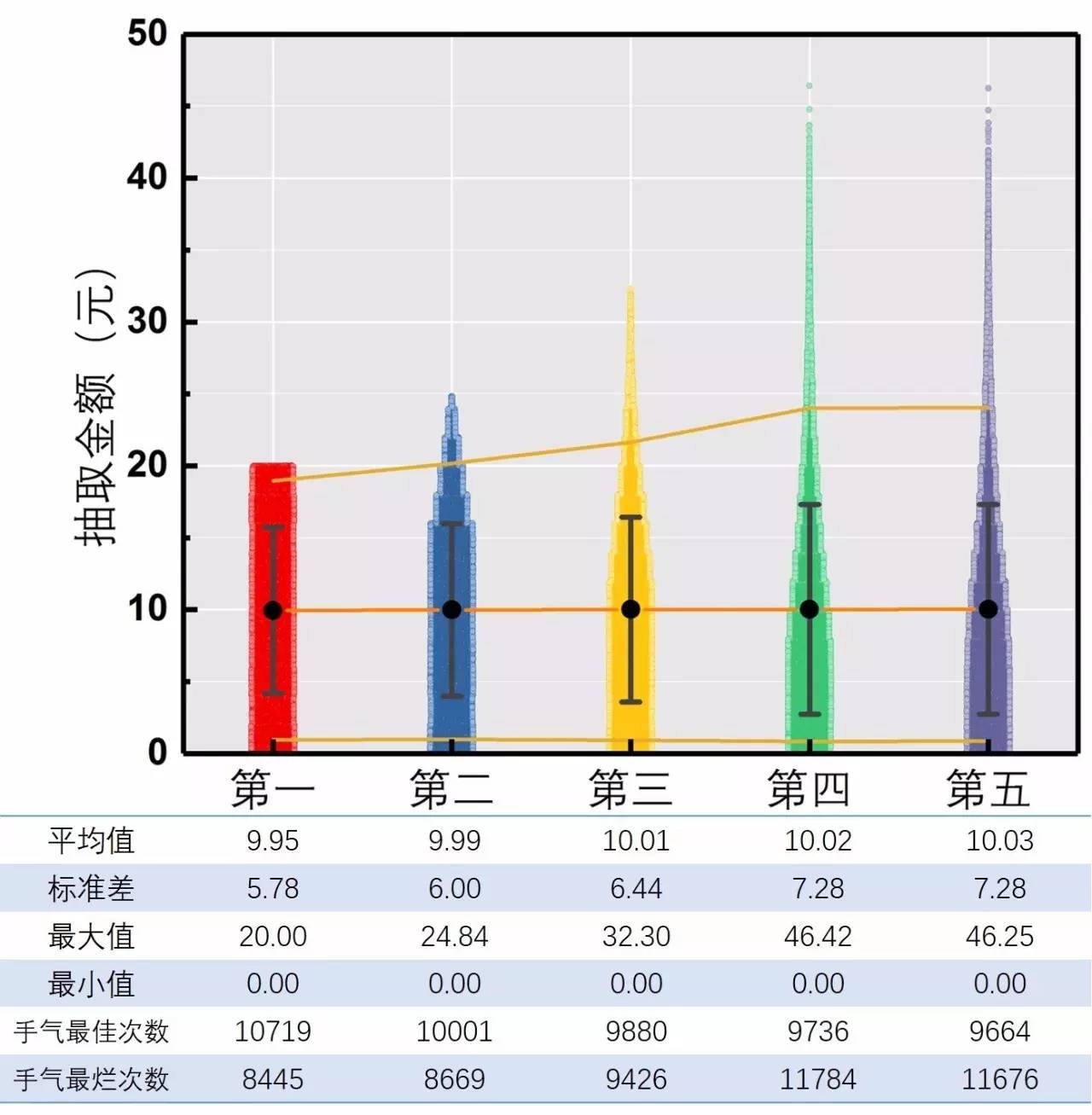
图9. 不一样前后顺序抢到的金额汇总(五万次模仿)
结果一切尽在掌控当中!均值相同,标准差变大,第一个人有最多的“手气最好”!
因为最近真的有人拉我玩“手气最好发红包”的游戏,吓得我赶忙给自己发了一千万个红包研究理论规律。
毕竟这个游戏里只抢不发闷声发大财是坠吼滴,一抽到手气最好之前抢的钱都空费了。
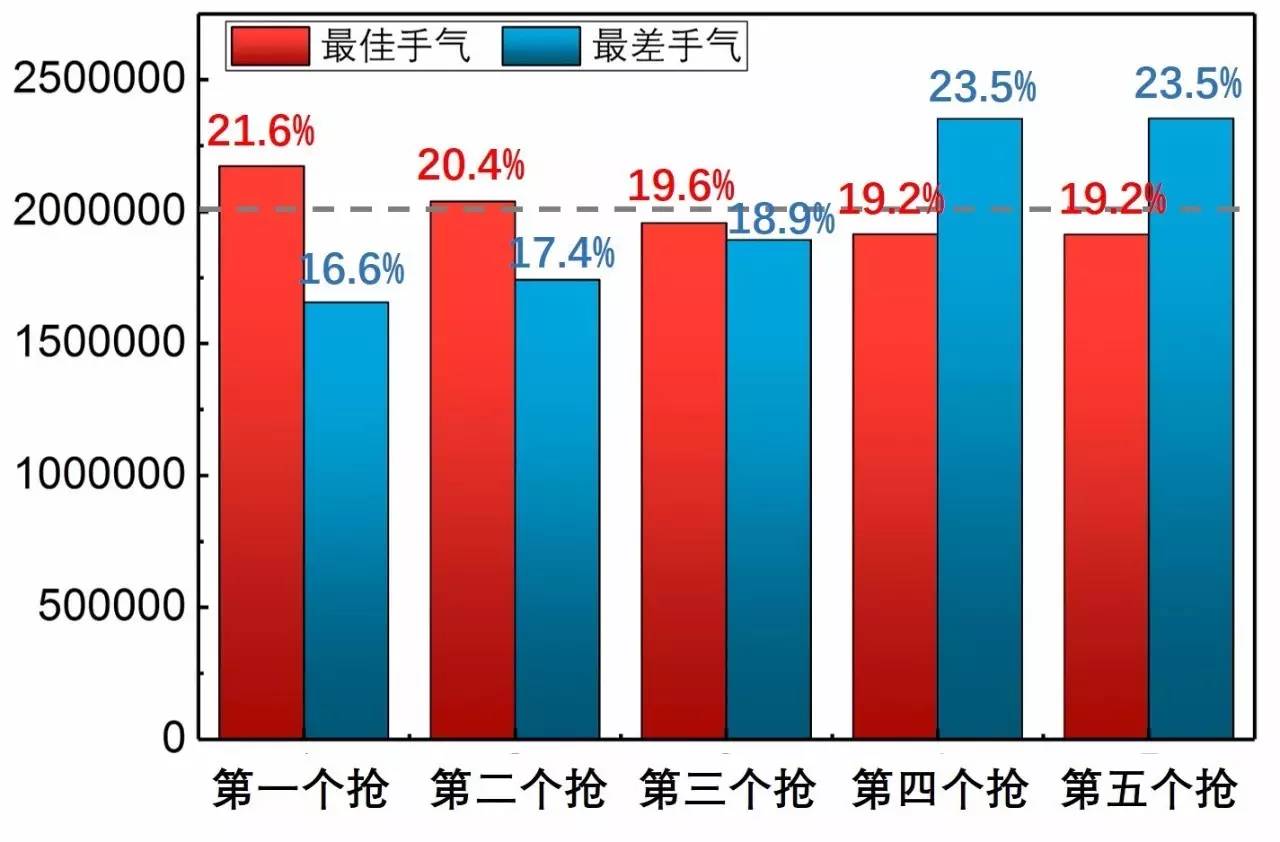
图10. 不一样前后顺序下抢到的手气最好、最差(一千万次模仿)
看来前后顺序对抽到“手气最好”是有决定性影响的!
5个人抢红包的时候,越先抽,抽到“手气最好”的几率越大!第1个人抢到手气最好的几率是21.6%,而最后俩人的几率只有19.2%!相反,第1个人抢到手气最差的几率是16.6%,最后俩人的几率高达23.5%!
可是只有5个人抢的时候有这个规律。
当参加抢红包的人数变化时,“手气最好”的几率跟随先抢后抢顺序变化的规律也是不一样的。
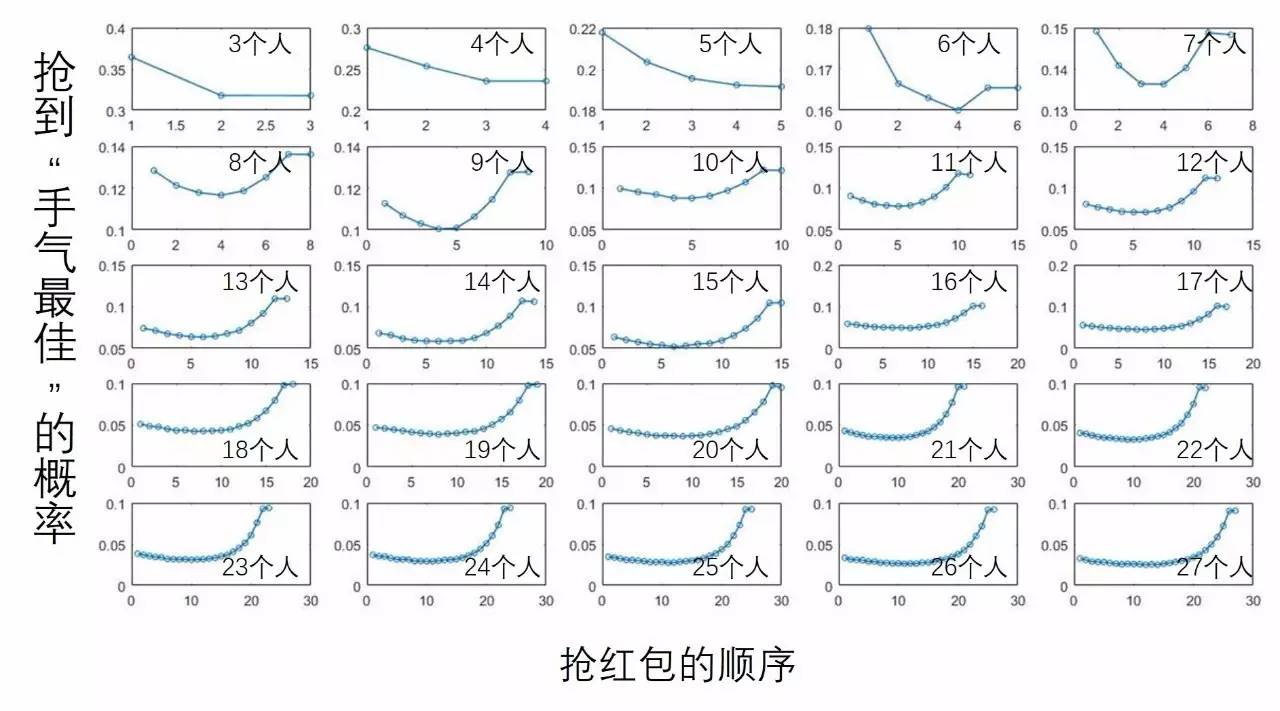
所以一帮人玩“手气最好发红包”的游戏时
3~5人时“手气最好”几率是随抢的顺序而下降的,所以毅然要憋到后面再抢!
6~15人时几率是先下降后增加的,所以要看准技能和机会,挤在中心的地位抢!
16人以上时基本是越往后几率越高,尽也许先抢!最后两个人拿到“手气最好”的几率极高!
七、结论
微信抢红包的规律
规则:每个人能抢到的金额屈服“0.01到2倍剩余均值”之间的随机散布。
均值:不管先抢后抢,均值都一样
标准差:后抢的标准差更大,也许抢到超级大红包,也也许抢到超级小红包
最大最小值:第一个抢抢不到大红包,后抢才也许抢到超级大红包
手气最好:和红包的个数是有关的,见第六部分
抢红包的最优战略是
风险偏好:假如你想要稳稳铛铛地抢,就先抢;假如你爱好抢到超级大红包,就后抢。
“手气最好发红包”游戏:发的红包数少就后抢,红包多就中心抢,很多就先抢!
通过这么漫长的系统研究我最终得出了最优战略!
我很高兴地去和他们玩“手气最好发红包”游戏了!
一帮辣鸡,在我壮大的几率论眼前臣服吧!
我能够利用最优战略,故意先憋几分钟再抢哈哈哈哈我真是太天赋了!

申谢
感激清华大学统计中心一名不肯透露姓名的热心同窗对本文理论推导部分的指点和关心。他严肃的科学立场,千锤百炼的工作风格,严谨的计算过程为本文提升了很多逼格。在此谨向他致以真挚的谢意!
参考文献
1、微信红包的架构设计简介,起源于QCon某高可用架构群整顿,整顿朱玉华
https://www.zybuluo.com/yulin718/note/93148
2、维基百科,Kolmogorov-Smirnov检验
https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test
3、维基百科,Anderson-Darling k-样本检验
https://en.wikipedia.org/wiki/Anderson%E2%80%93Darling_test
4、平均散布贝叶斯估量
Minka T P. Bayesian inference of a uniform distribution[R]. Technical report, MIT, 2001.
你也许还想看一些
理工男道貌岸然乱说八道的文章
下一场雾霾到来之前,除过戴口罩,我们还能咋办?
一个清华博士在供暖前给广大学子最中肯的建议
连诱骗女朋友都不会,你也好意思说自己是工程师?
理论分析:为何感到这个国庆节假期结婚的人特别多?
↑戳上方二维码关注毕导
也许是脑洞最奇异的科学段子手
郑重声明:此文内容为本网站转载企业宣传资讯,目的在于传播更多信息,与本站立场无关。仅供读者参考,并请自行核实相关内容。

